
0x01 从随机变量说起
假设有一枚硬币,将其抛出,落下后朝上的面为y。
这里的y是对未知量的一个表示。但它的值却是不确定的,可能取正面和反面两个值。
类似的不确定变量还有好多,比如说,将人的身高设为z,z中也包含了不确定性,因为不同的人身高是不一样的。
这类包含不确定性的变量我们称为随机变量。统计学就是研究这类不确定性变量的工具。
刻画随机变量最有力的一个工具就是它的概率分布。关于什么是概率分布,这里就不多说了,可以百度百科。
有了概率分布,我们可以说对一个随机变量有了完全的掌握,因为我们可以知道它可能取哪些值,某个值的概率是多少。
以上,是对基础知识的简单复习,下面开始进入正题。
0x02 什么是熵?
上面,我们知道,概率分布是对随机变量的刻画,不同的随机变量有着相同或不同的概率分布,熵,就是对不同概率分布的刻画!
为什么我们还需要对不同的概率分布进行刻画?本质上,是为了描述不确定的程度,并以此对不同的概率分布进行比较。
请允许我举个栗子。
假如我告诉你,我有两枚硬币,一个上抛一次正面朝上概率是 0.5,另一个是 0.8。此时,假设两枚硬币上抛一次落下后朝上的面分别是x,y。此时,我们可以很容易确定随机变量x,y的概率分布,并借此对两个随机变量有准确的掌握。
但我们要问,这两个随机变量哪个更随机?或者说,哪个随机变量包含的不确定性更大?
如果发挥直觉,我们可以感觉到,正面朝上概率为 0.8 的概率分布不确定性小于正面朝上概率为 0.5 的不确定性。
进一步思考,我们为什么会有这样的直觉?
因为我们是从“使用”概率分布的角度来思考问题的。也就是说,如果我们知道一枚硬币抛出后正面朝上概率为 0.8,要比知道概率为 0.5,更容易猜对硬币抛出后哪面朝上。换句话说,0.8 的概率分布比 0.5 的概率分布对我们来说,具有更大的信息量。
现在,我们对概率分布中的不确定性有了感性的认识,现在需要的是一个定量的指标,来衡量这个不确定性。想必你已经猜到了,这个指标就是熵。
0x03 熵的数学表达
熵应该是什么样子,才能表达出概率分布中的不确定性呢?
为了解决这个问题,我们来考察一下概率分布中的某个取值,以抛硬币为例,我们看正面这个取值。可以看到,取正面的概率越大,则不确定性就越小。概率越大,不确定性越小!请把这句话在心中默念三遍。能够表达出概率越大,不确定性越小的表达式就是:
-log(p)
为了让大家有一个感性的认识,我特意画了一个图:
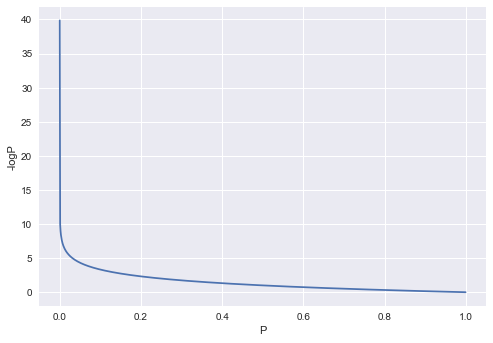
上图中的纵轴为 -logP,横轴为 P。
然后,我们继续思考,上面的 -logP 只是衡量了某个概率的不确定性,一个概率分布包含多个概率,而且概率相加等于1,一个概率大,必然会有其他的概率小。还是以抛硬币为例,0.8 概率的正面,不确定性固然很小,但同时会造成反面的概率为 0.2,不确定性比较大。这意味着,我们猜对一次抛硬币正面朝上的难度比较小,但要猜对一次反面朝上的难度就比较大。很显然,我们要衡量一个概率的分布的不确定性,就要综合衡量所有概率表达的不确定性。也就是求一个概率分布综合的不确定性。当当当当当!熵正式出场!
-∑plog(p)
这个指标可以理解成概率分布的不确定性的期望值。这个值越大,表示该概率分布不确定性越大。它为我们人类提供的“信息”就越小,我们越难利用这个概率分布做出一个正确的判断。从这个角度,我们可以看到,熵是对概率分布信息含量的衡量,这与它是不确定性的衡量,其实是两种解读方式而已。
0x04 伯努利分布的熵
对于抛硬币判正反面来说,它的概率分布是伯努利分布,我们假设正面朝上的概率为p,则反面朝上的概率为(1-p),它的熵就是:
H(p) = -plog(p) -(1-p)log(1-p)
我们把它画出来就是这样。
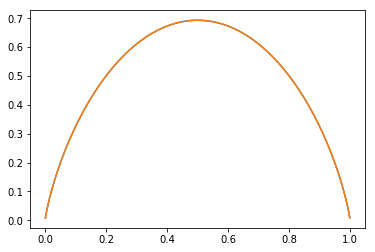
可以看到,p=0.5时,伯努利分布的熵达到最大。这与我们的经验常识一致,因为此时,硬币朝上还是朝下完全是随机的,不确定性最大。
当p趋向于0时,熵也趋向于0,举个极端例子,如果硬币以概率1正面朝上,概率0反面朝上,则完全没有不确定性,所以熵就是0,因为熵是对不确定性的一个测量。
再来思考一个问题,我们说熵是描述不确定性的,在概率论中,不是有一个方差可以用来描述变量变化程度的吗,它和熵是什么关系呢?
直觉上,方差越大,不确定性就越大,熵就应该越大,事实上确实如此,请看下图:
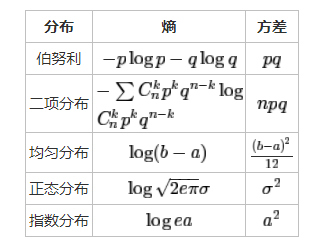
对我们投硬币的伯努利分布,方差pq的最大值在p=0.5时取得,由上文我们知道,这也是熵取得最大值的p值。
对于正态分布,我们可以看到,期望对熵没有影响,只有方差才对熵有影响。这于我们的直觉也是相符的。
以上,我们尽可能从直觉的角度分析出了熵的表达式,也查看了几种分布的熵,以及它们和该分布的方差的关系,发现二者要描述的含义具有内在一致性。至此,我们终于可以说一窥熵的庐山真面目了。
0xFF 总结
以上是我们要讨论的第一部分内容,下面,我们要讨论由熵引出的各种其他熵,也就是本文文首提出的那些。
Refer:
[1] 机器学习面试之各种混乱的熵(一)
[2] 机器学习面试之各种混乱的熵
[3] 春招已近,这份 GitHub 万星的 ML 算法面试大全请收下